What is CherryTrail (Braswell)?
“CherryTrail” (CYT) is the next generation Atom “APU” SoC from Intel (v3 2015) replacing the current Z3000 “BayTrail” (BYT) SoC which was Intel’s major foray into tablets (both Windows & Android). The “desktop” APUs are known as “Braswell” (BRS) while the APUs for other platforms have different code names.
BayTrail was a major update both CPU (OOS core, SSE4.x, AES HWA, Turbo/dynamic overclocking) and GPU (EV7 IvyBridge GPGPU core) so CherryTrail is a minor process shrink – but with a very much updated GPGPU – updated to EV8 (as latest Core Broadwell).
In this article we test (GP)GPU graphics unit performance; please see our other articles on:
Hardware Specifications
We are comparing the internal GPUs of 3 processors (BayTrail, CherryTrail and Broadwell-Y) that support GPGPU.
| Graphics Unit |
BayTrail GT |
CherryTrail GT |
Broadwell GT2Y – HD 5300 |
Comment |
| Graphics Core |
B-GT EV7 |
B-GT EV8? |
B-GT2Y EV8 |
CherryTrail’s GPU is meant to be based on EV8 like Broadwell – the very latest GPGPU core from Intel! This makes it more advanced than the very popular Core Haswell series, a first for Atom. |
| APU / Processor |
Atom Z3770 |
Atom X7 Z8700 |
Core M 5Y10 |
Core M is the new Core-Y UULV versions for high-end tablets against the Atom processors for “normal” tablets/phones. |
| Cores (CU) / Shaders (SP) / Type |
4C / 32SP (2×4 SIMD) |
16C / 128SP (2×4 SIMD) |
24C / 192SP (2×4 SIMD) |
Here’s the major change: CherryTrail has no less than 4 times the compute units (CU) in the same power envelope of the old BayTrail. Broadwell has more (24) but it is also rated at higher TDP. |
| Speed (Min / Max / Turbo) MHz |
333 – 667 |
200 – 600 |
200 – 800 |
CherryTrail goes down all the way to 200MHz (same as Broadwell) which should help power savings. Its top speed is a bit lower than BayTrail but not by much. |
| Power (TDP) W |
2.4 (under 4) |
2.4 (under 4) |
4.5 |
Both Atoms have the same TDP of around 2-2.4W – while Broadwell-Y is rated at 2x at 4.5-6W. We shall see whether this makes a difference. |
| DirectX / OpenGL / OpenCL Support |
11 / 4.0 / 1.1 |
11.1 (12?) / 4.3 / 1.2 |
11.1 (12?) / 4.3 / 2.0 |
Intel has continued to improve the video driver – 2 generations share a driver – but here CherryTrail has a brand-new driver that supports much newer technologies like DirectX 11.1 (vs 11.0), OpenGL 4.3 (vs 4.0) including Compute and OpenCL 1.2. Broadwell’s driver does support OpenCL 2.0 – perhaps a later CherryTrail driver will do too? |
| FP16 / FP64 Support |
No / No (OpenCL), Yes (DirectX) |
No / No (OpenCL), Yes (DirectX, OpenGL) |
No / No (OpenCL), Yes (DirectX, OpenGL) |
Sadly FP16 support is still missing and FP64 is also missing on OpenCL – but available in DirectX Compute as well as OpenGL Compute! Those Intel FP64 extensions are taking their time to appear… |
GPGPU Performance
We are testing vectorised, crypto (including hash), financial and scientific GPGPU performance of the GPUs in OpenCL, DirectX ComputeShader and OpenGL ComputeShader (if supported).
Results Interpretation: Higher values (MPix/s, MB/s, etc.) mean better performance.
Environment: Windows 8.1 x64, latest Intel drivers (Jun 2015). Turbo / Dynamic Overclocking was enabled on all configurations.
| Graphics Processors |
BayTrail GT |
CherryTrail GT |
Broadwell GT2Y – HD 5300 |
Comments |
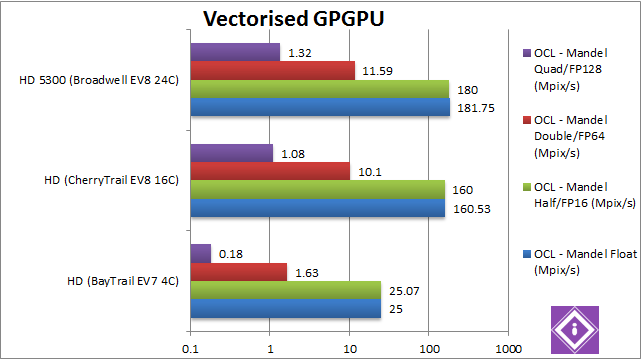 |
 |
Single/Float/FP32 Vectorised OpenCL (Mpix/s) |
25 |
160 [+6.4x] |
181 [+13%] |
Straight off the bat we see that 4x more advanced CUs in CherryTrail gives us 6.4x better performance a huge improvement! Even the brand-new Broadwell GPU is only 13% faster. |
 |
Half/Float/FP16 Vectorised OpenCL (Mpix/s) |
25 |
160 [+6.4x] |
180 [+13%] |
As FP16 is not supported by any of the GPUs and promoted to FP32 the results don’t change. |
 |
Double/FP64 Vectorised OpenCL (Mpix/s) |
1.63 (emulated) |
10.1 [+6.2x] (emulated) |
11.6 [+15%] (emulated) |
None of the GPUs support native FP64 either: emulating FP64 (mantissa extending) is quite hard on all GPUs, but the results don’t change: CherryTrail is 6.2x faster with Broadwell just 15% faster. |
 |
Quad/FP128 Vectorised OpenCL (Mpix/s) |
0.18 (emulated) |
1.08 [+6x] (emulated) |
1.32 [+22%] (emulated) |
Emulating FP128 using FP32 is even more complex but CherryTrail does not disappoint, it is still 6x faster; Broadwell does pull ahead a bit being 22% faster. |
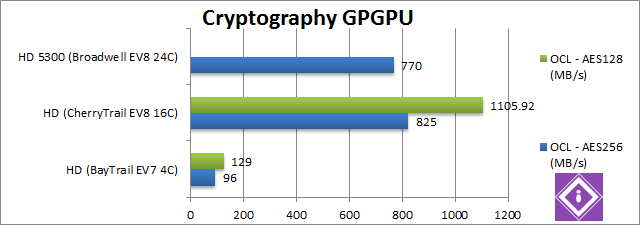 |
 |
AES256 Crypto OpenCL (MB/s) |
96 |
825 [+8.6x] |
770 [-7%] |
In this tough integer workload that uses shared memory CherryTrail does even better – it is 8.6x faster, more than we’d expect – the newer driver may help. Surprisingly this is faster than even Broadwell. |
 |
AES128 Crypto OpenCL (MB/s) |
129 |
1105 [+8.6x] |
n/a |
What we saw before is no fluke, CherryTrail’s GPU is still 8.6 times faster than BayTrail’s. |
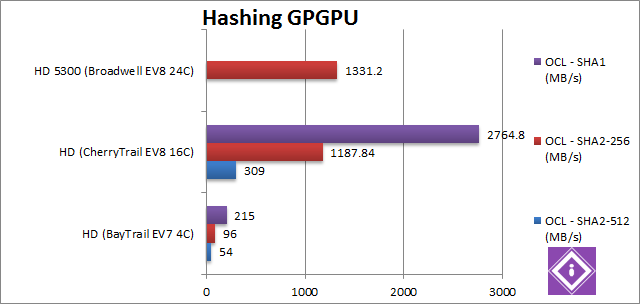 |
 |
SHA2-512 (int64) Hash OpenCL (MB/s) |
54 |
309 [+5.7x] |
|
This 64-bit integer compute-heavy wokload is hard on all GPUs (no native 64-bit arithmetic), but CherryTrail does well – it is almost 6x faster than the older BayTrail. Note that neither DirectX nor OpenGL natively support int64 so this is about as hard as it gets for our GPUs. |
 |
SHA2-256 (int32) Hash OpenCL (MB/s) |
96 |
1187 [+12.4x] |
1331 [+12%] |
In this integer compute-heavy workload, CherryTrail really shines – it is 12.4x (twelve times) faster than BayTrail! Again, even the latest Broadwell is just 12% faster than it! Atom finally kicks ass both in CPU and GPU performance. |
 |
SHA1 (int32) Hash OpenCL (MB/s) |
215 |
2764 [+12.8x] |
|
SHA1 is less compute-heavy, but results don’t change: CherryTrail is 12.8x times faster – the best result we’ve seen so far. |
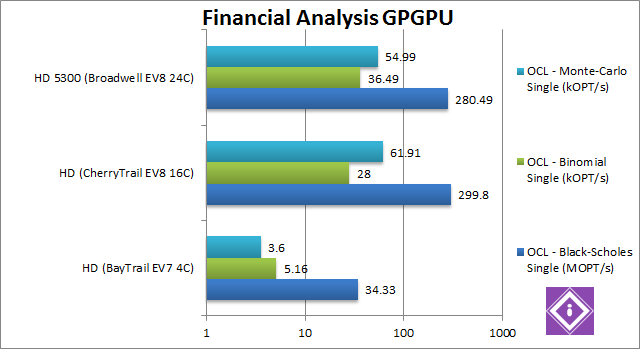 |
 |
Black-Scholes FP32 OpenCL (MOPT/s) |
34.33 |
299.8 [+8.7x] |
280.5 [-7%] |
Starting with the financial tests, CherryTrail is quick off the mark – being almost 9x (nine times) faster than BayTrail – and again somehow faster than even Broadwell. Who says Atom cannot hold its own now? |
 |
Binomial FP32 OpenCL (kOPT/s) |
5.16 |
28 [+5.4x] |
36.5 [+30%] |
Binomial is far more complex than Black-Scholes, involving many shared-memory operations (reduction) – but CherryTrail still holds its own, it’s over 5x times faster – not as much as we saw before but massive improvement. Broadwell’s EV8 GPU does show its prowess being 30% faster still. |
 |
Monte-Carlo FP32 OpenCL (kOPT/s) |
3.6 |
61.9 [+17x] |
54 [-12%] |
Monte-Carlo is also more complex than Black-Scholes, also involving shared memory – but read-only; here we see Broadwell shine – it’s 17x (seventeen times) faster than BayTrail’s GPU – so much so we had to recheck. Most likely the newer GPU driver helps – but BayTrail will not get these improvements. Broadwell is again surprisingly 12% slower. |
 |
 |
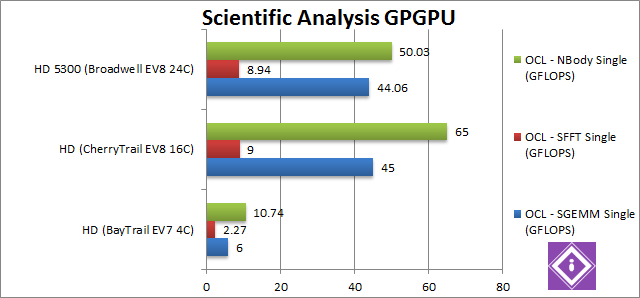
SGEMM FP32 OpenCL (GFLOPS) |
6 |
45 [+7.5x] |
44.1 [-3%] |
GEMM is quite a tough algorithm for our GPUs but CherryTrail remains over 7.5x faster – even Broadwell is 3% slower than it. We saw before EV8 not performing as we expected – perhaps some more optimisations are needed. |
 |
SFFT FP32 OpenCL (GFLOPS) |
2.27 |
9 [+3.96x] |
8.94 [-1%] |
FFT involves many kernels processing data in a pipeline – so here we see CherryTrail only 4x (four times) faster – the slowest we’ve seen so far. But then again Broadwell scores about the same so it’s a tough test for all GPUs. |
 |
N-Body FP32 OpenCL (GFLOPS) |
10.74 |
65 [+6x] |
50 [-23%] |
In our last test we see CherryTrail going back to being 6x faster than BayTrail – surprisingly again Broadwell’s EV8 GPU is 23% slower than it. |
There is no simpler way to put this: CherryTrail Atom’s GPU obliterates the old one – never being less than 4x and up to 17x (yes, seventeen!) faster, many times even overtaking the much newer, more expensive and more power hungry Broadwell (Core M) EV8 GPU! It is a no-brainer really, you want it – for once Microsoft made a good choice for Surface 3 after the disasters of earlier Surfaces (perhaps they finally learn? Nah!).
There isn’t really much to criticise: sure, FP16 native support is missing – which is a pity on Android (that uses FP16 in UX) and naturally FP64 is also missing – though as usual DirectX compute and OpenGL compute. As mentioned, since OpenGL 4.3 is supported, Compute is also supported for the first time on Atom – a feature recently introduced in newer drivers on Haswell and later GPUs (EV7.5, EV8).
Just in case we’re not clear: this *is* the Atom you are looking for!
Transcoding Performance
We are testing memory performance of GPUs using their hardware transcoders using popular media formats: H.264/MP4, AVC1, M.265/HEVC.
Results Interpretation: Higher values (MPix/s, MB/s, etc.) mean better performance. Lower values (ns, clocks) mean better performance.
Environment: Windows 8.1 x64, latest Intel drivers (June 2015). Turbo / Dynamic Overclocking was enabled on all configurations.
| Graphics Processors |
BayTrail GT |
CherryTrail GT |
Broadwell GT2Y – HD 5300 |
Comments |
| H.264/MP4 Decoder/Encoder |
QuickSync H264 (hardware accelerated) |
QuickSync H264 (hardware accelerated) |
QuickSync H264 (hardware accelerated) |
Same transcoder is used for all GPUs. |
 |
 |
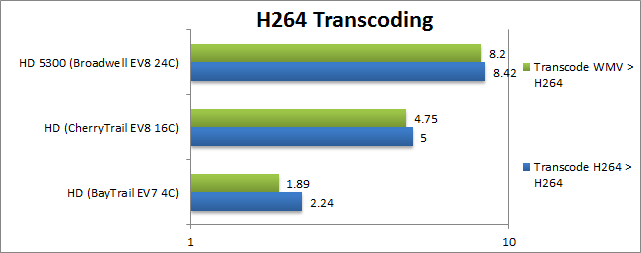
H264 > H264 Transcoding (MB/s) |
2.24 |
5 [+2.23x] |
8.41 [+68%] |
H.264 transcoding on the new Atom has more than doubled (2.2x) which makes it ideal as a HTPC (e.g. Plex server). However, with more power we can see that Core M has over 60% more bandwidth. |
 |
WMV > H264 Transcoding (MB/s) |
1.89 |
4.75 [+2.51x] |
8.2 [+70%] |
When just using the H264 encoder we still see a 2.5x improvement (over two and a half times), with Core M again about 70% faster still. |
Intel has not forgotten transcoding, with the new Atom over 2x (twice) as fast – so if you were thinking of using it as a HTPC (NUC/Brix) server, better get the new one. However, unless you really want low power – the Core M (and thus ULV) versions have are 60-70% faster still…
GPGPU Memory Performance
We are testing memory performance of GPUs using OpenCL, DirectX ComputeShader and OpenGL ComputeShader (if supported), including transfer (up/down) to/from system memory and latency.
Results Interpretation: Higher values (MPix/s, MB/s, etc.) mean better performance. Lower values (ns, clocks) mean better performance.
Environment: Windows 8.1 x64, latest Intel drivers (June 2015). Turbo / Dynamic Overclocking was enabled on all configurations.
| Graphics Processors |
BayTrail GT |
CherryTrail GT |
Broadwell GT2Y – HD 5300 |
Comments |
| Memory Configuration |
2GB DDR3 1067MHz 64/128-bit (shared with CPU) |
4GB DDR3 1.6GHz 64/128-bit (shared with CPU) |
4GB DDR3 1.6GHz 128-bit (shared with CPU) |
Atom is generally configured to use a single memory controller, but CherryTrail runs at 1.6Mt/s same as modern Core APUs. But Core M/Broadwell naturally has a dual-channel controller though some laptops/tablets may use just one. |
| Cache Configuration |
32kB L2 global/texture? 128kB L3 |
256kB L2 global/texture? 384kB L3 |
256kB L2 global/texture? 384kB L3 |
Internal cache arrangement seems to be very secret – so a lot of it is deduced from the latency graphs. The L2 increase in CherryTrail is in line with CU increase, i.e. 8x larger. |
 |
 |
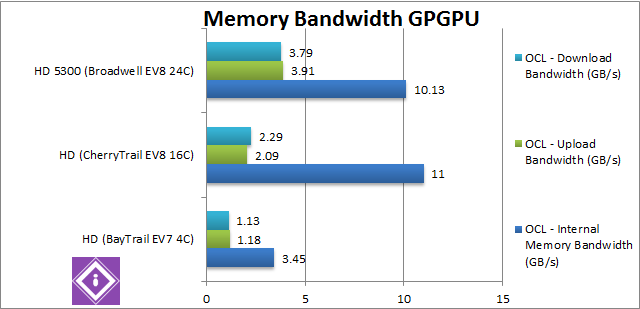
Internal Memory Bandwidth (GB/s) |
3.45 |
11 [+3.2x] |
10.1 [-8%] |
CherryTrail manages over 3x higher bandwidth during internal transfer over BayTrail, close to what we’d expect a dual-channel system to achieve. Surprisingly our dual-channel Core M manages to be 8% slower. We did see Broadwell achieve less than Haswell – which may explain what we’re seeing here. |
 |
Upload Bandwidth (GB/s) |
1.18 |
2.09 [+77%] |
3.91 [+87%] |
While all APUs don’t need to transfer memory over PCIe like dedicated GPUs, they still don’t support “zero copy” – thus memory transfers are not free. Here CherryTrail improves almost 2x over BayTrail – but finally we see Core M being 87% faster still. |
 |
Download Bandwidth (GB/s) |
1.13 |
2.29 [+2.02x] |
3.79 [+65%] |
While upload bandwidth was the same, download bandwidth has improved a bit more, with CherryTrail being over 2x (twice) faster – but again Broadwell is 65% faster still. This will really help GPGPU applications that need to copy large results from the GPU to CPU memory until “zero copy” feature arrives. |
 |
 |
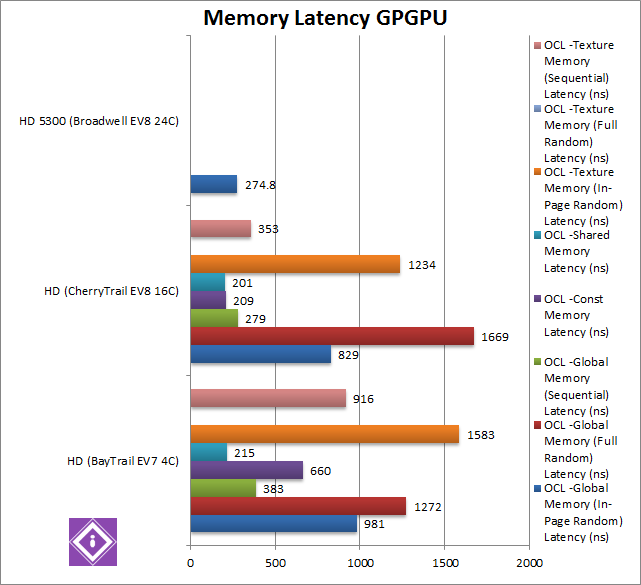
Global Memory (In-Page Random) Latency (ns) |
981 |
829 [-15%] |
274 |
With the memory running faster, we see latency decreasing by 15% a good result. However, Broadwell does so much better with almost 1/4 latency. |
 |
Global Memory (Full Random) Latency (ns) |
1272 |
1669 [+31%] |
|
Surprisingly, using full-random access we see latency increase by 31%. This could be due to the larger (4GB vs. 2GB) memory arrangement – the TLB-miss hit could be much higher. |
 |
Global Memory (Sequential) Latency (ns) |
383 |
279 [-27%] |
|
Sequential access brings the latency down by 27% – a good result. |
 |
Constant Memory Latency (ns) |
660 |
209 [-1/3x] |
|
With L1 cache covering the entire constant memory on CherryTrail – we see latency decrease to 1/3 (a third), great for kernels that use more than 32kB constant data. |
 |
Shared Memory Latency (ns) |
215 |
201 [-6%] |
|
Shared memory is a bit faster (6% lower latency), nothing to write home about. |
 |
Texture Memory (In-Page Random) Latency (ns) |
1583 |
1234 [-22%] |
|
With the memory running faster, as with global memory we see latency decreasing by 22% here – a good result! |
 |
Texture Memory (Sequential) Latency (ns) |
916 |
353 [-61%] |
|
Sequential access brings the latency down by a huge 61%, an even bigger difference than what we saw with Global memory. Impressive! |
Again, we see big gains in CherryTrail with bandwidth increasing by 2-3x which is necessary to keep all those new EVs fed with data; Broadwell does do better but then again it has a dual-channel memory controller.
Latency has also decreased by a good amount 6-22% likely due to the faster memory employed, and the much larger caches (8x) do help. For data that exceeded the small BayTrail cache (32kB) – the CherryTrail one should be more than sufficient.
Shader Performance
We are testing shader performance of the GPUs in DirectX and OpenGL.
Results Interpretation: Higher values (MPix/s, MB/s, etc.) mean better performance.
Environment: Windows 8.1 x64, latest Intel drivers (Jun 2015). Turbo / Dynamic Overclocking was enabled on all configurations.
| Graphics Processors |
BayTrail GT |
CherryTrail GT |
Broadwell GT2Y – HD 5300 |
Comments |
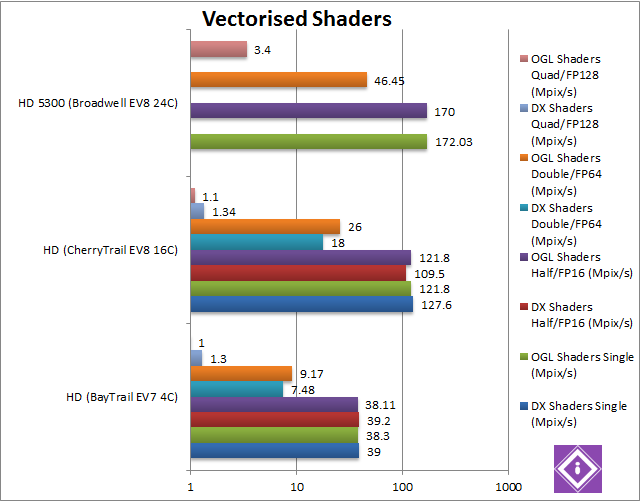 |
 |
Single/Float/FP32 Vectorised DirectX (Mpix/s) |
39 |
127.6 [+3.3x] |
|
Starting with DirectX FP32, CherryTrail is over 3.3x faster than BayTrail – not as high as we saw before but a good start. |
 |
Single/Float/FP32 Vectorised OpenGL (Mpix/s) |
38.3 |
121.8 [+3.2x] |
172 [+41%] |
OpenGL does not change matters, CherryTrail is still just over 3x (three times) faster than BayTrail. Here, though, Broadwell is 41% faster still… |
 |
Half/Float/FP16 Vectorised DirectX (Mpix/s) |
39.2 |
109.5 [+2.8x] |
|
As FP16 is not supported by any of the GPUs and promoted to FP32 the results don’t change. |
 |
Half/Float/FP16 Vectorised OpenGL (Mpix/s) |
38.11 |
121.8 [+3.2x] |
170 [+39%] |
As FP16 is not supported by any of the GPUs and promoted to FP32 the results don’t change. |
 |
Double/FP64 Vectorised DirectX (Mpix/s) |
7.48 |
18 [+2.4x] |
|
Unlike OpenCL driver, DirectX driver does support FP64 – so all GPUs run native FP64 code not emulation. Here, CherryTrail is only 2.4x faster than BayTrail. |
 |
Double/FP64 Vectorised OpenGL (Mpix/s) |
9.17 |
26 [+2.83x] |
46.45 [+78%] |
As above, OpenGL driver does support FP64 also – so all GPUs run native FP64 code again. CherryTrail is 2.8x times faster here, but Broadwell is 78% faster still. |
 |
Quad/FP128 Vectorised DirectX (Mpix/s) |
1.3 (emulated) |
1.34 [+3%] (emulated) |
(emulated) |
Here we’re emulating (mantissa extending) FP128 using FP64 not FP32 but it’s hard: CherryTrail’s performance falls to just 3% faster over BayTrail, perhaps some optimisations are needed. |
 |
Quad/FP128 Vectorised OpenGL (Mpix/s) |
1 (emulated) |
1.1 [+10%] (emulated) |
3.4 [+3.1x] (emulated) |
OpenGL does not change the results – but here we see Broadwell being 3x faster than both CherryTrail and BayTrail. Perhaps such heavy shaders are too much for our Atom GPUs. |
Unlike GPGPU, here we don’t see the same crushing improvement – but CherryTrail’s GPU is still about 3x (three times) faster than BayTrail’s – though Broadwell shows its power. Perhaps our shaders are a bit too complex for pixel processing and should rather stay in the GPGPU field…
Shader Memory Performance
We are testing memory performance of GPUs using DirectX and OpenGL, including transfer (up/down) to/from system memory.
Results Interpretation: Higher values (MPix/s, MB/s, etc.) mean better performance.
Environment: Windows 8.1 x64, latest Intel drivers (June 2015). Turbo / Dynamic Overclocking was enabled on all configurations.
| Graphics Processors |
BayTrail GT |
CherryTrail GT |
Broadwell GT2Y – HD 5300 |
Comments |
 |
 |
Internal Memory Bandwidth (GB/s) |
6.74 |
11.18 [+65%] |
12.46 [+11%] |
DirectX bandwdith is not as “bad” as OpenCL on BayTrail (better driver?) so we start from a higher baseline: CherryTrail still manages 65% more bandwidth – with Broadwell only squeezing 11% more despite its dual-channel. It shows that OpenCL GPGPU driver has come a long way to match DirectX. |
 |
Upload Bandwidth (GB/s) |
2.62 |
2.83 [+8%] |
5.29 [+87%] |
While all APUs don’t need to transfer memory over PCIe like dedicated GPUs, they still don’t support “zero copy” – thus memory transfers are not free. Again BayTrail does better so CherryTrail can only be 8% faster than it – with Broadwell finally 87% faster. |
 |
Download Bandwidth (GB/s) |
1.14 |
2.1 [+83%] |
1.23 [-42%] |
Here BayTrail “stumbles” so CherryTrail can be 83% faster with Broadwell surprisingly 42% slower. What it does show is that the CherryTrail drivers are better despite being much newer. It is a pity Intel does not provide this driver for BayTrail too… |
Again, we see big gains in CherryTrail with bandwidth increasing by 2-3x which is necessary to keep all those new EVs fed with data; Broadwell does do better but then again it has a dual-channel memory controller.
SiSoftware Official Ranker Scores
Final Thoughts / Conclusions
Here we tested the brand-new Atom X7 Z8700 (CherryTrail) GPU with 16 EVs (EV8) – 4x (four times) more than the older Atom Z3700 (BayTrail) GPU with 4 EVs (EV7) – so we expected big gains – and they were delivered: GPGPU performance is nothing less than stellar, obliterating the old Atom GPU to dust – no doubt also helped by the newer driver (which sadly BayTrail won’t get). And all at the same TDP of about 2.4-5W! Impressive!
Even the very latest Core M (Broadwell) GPU (EV8) is sometimes left behind – at about 2x higher power, more EVs and higher cost – perhaps the new Atom is too good?
Architecturally nothing much has changed (beside the far more EVs) – but we also get better bandwidth and lower latencies – no doubt due to higher memory bus clock.
All in all, there’s no doubt – this new Atom is the one to get and will bring far better graphics and GPGPU performance at low cost – even overshadowing the great Core M series – no doubt the reason it is found in the latest Surface 3.
To see how the Atom CherryTrail CPU fares, please see CPU Atom Z8700 (CherryTrail) performance article!



















